Resumen 📖
📌 En el artículo anterior (Workflows Parte 1/2), se mostró de manera introductoria cómo crear modelos, recetas y workflows dentro del ecosistema tidymodels 🙌. En este post se mostrarán aplicaciones más avanzadas de los workflows 🔁 y recetas 🍳, específicamente a través de los siguientes casos de uso:
-
Discretización de localizaciones 📐(lat/long) con modelos predictivos.
-
Pivot de puntos en el mapa 🗺 (estadios ⚽ de Boca y River)
-
Reemuestreo espacial 🧪
👉🏻 Se continuara utilizando el conjunto de datos referente a los delitos ocurridos en la ciudad de Buenos Aires, almacenado en sknifedatar 📦.
Libraries 📚
library(tidymodels)
library(tidyverse)
library(leaflet)
library(embed)
#install.packages("devtools")
#devtools::install_github("rafzamb/sknifedatar")
library(sknifedatar)
Discretización de variables con modelos predictivos 📐
❗En el siguiente gráfico se observan las esquinas de CABA, además se agrega el número de delitos registrados durante los últimos 12 meses (situándonos en diciembre del 2019) en sus cercanías.
esquinas_plot <- sknifedatar::data_crime_clime %>%
filter(pliegue == 13) %>%
mutate(delitos_last_12 = ifelse(delitos_last_12 > 200,
200,delitos_last_12))
ggplot(esquinas_plot, aes(x = long, y = lat), color = delitos_last_12) +
geom_point(aes(colour = delitos_last_12)) +
scale_color_gradient(low = "yellow", high = "red") +
theme_minimal()
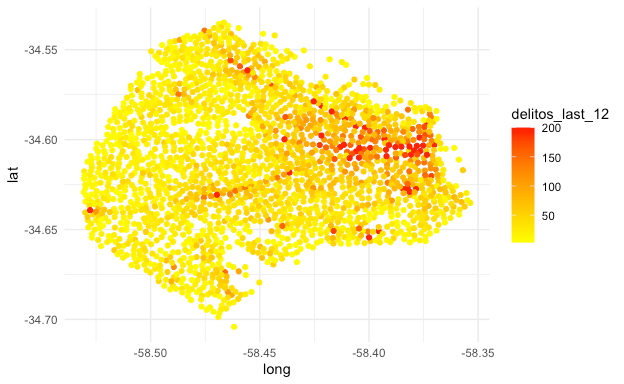
🔎 Si se busca segmentar o discretizar las esquinas en función de la relación entre la longitud y la ocurrencia de delitos 🚨, podríamos hacerlo a través de un modelo predictivo. Por ejemplo:
Receta_xgb <- recipe(esquinas_plot) %>%
step_discretize_xgb(long, outcome = "delitos_last_12") %>%
prep()
👉🏻 La función step_discretize_xgb() realiza una discretización a través de un modelo de Extreme Gradient Boosting (XGBoost) 🤖, este requiere que se especifique la(s) variable a discretizar, además de la variable dependiente para ajustar el modelo.
📌 El ajuste se realiza con los parámetros por defecto, para aplicaciones más avanzadas se pueden optimizar los hiperparámetros del XGB para la discretización 💡, solo se debe agregar la función tune() a la receta y realizar el ajuste, este tópico está fuera del alcance de este post. A continuación, observamos los cortes generados.
cortes <- tidy(Receta_xgb, number = 1) %>% pull(values)
print(cortes)
[1] -58.50687 -58.49070 -58.47886 -58.46836 -58.45613 -58.44208
[7] -58.42655 -58.40848 -58.38719
🔎 Estos valores representan los puntos de longitud óptimos para segmentar las esquinas en función de los crímenes registrados. Horneando 🍳 la receta sobre los datos, se muestra la variable long discretizada para cada esquina 📍.
bake(Receta_xgb, new_data = esquinas_plot, c(id, long)) %>% head()
# A tibble: 6 x 2
id long
<fct> <fct>
1 esquina_1 [-58.48,-58.47)
2 esquina_10 [-58.41,-58.39)
3 esquina_100 [-58.51,-58.49)
4 esquina_1001 [-58.51,-58.49)
5 esquina_1002 [-58.51,-58.49)
6 esquina_1003 [-Inf,-58.51)
📌 Para entender el objetivo de la discretización, se muestra el mismo mapa de las esquinas de CABA, pero agregando la discretización por zonas en función de la longitud y ocurrencia delictiva en los últimos 12 meses.
ggplot(esquinas_plot, aes(x = long, y = lat), color = delitos_last_12) +
geom_vline(xintercept = cortes, col = "blue", alpha = 0.7) +
geom_point(aes(colour = delitos_last_12), alpha = 0.5) +
scale_color_gradient(low = "yellow", high = "red") +
theme_bw()
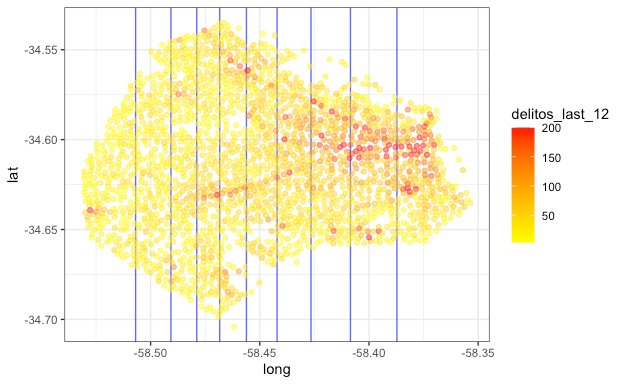
⚠️ ¿Tiene algún fundamento la implementación de esta discretización?
No, simplemente sirve para mostrar una de las tantas cosas que podemos hacer ✅. Sin embargo, en el caso de requerir realizar segmentaciones en función a otras variables, esta puede ser una opción.
👉🏻 Aunque en esta oportunidad solo se discretizo la longitud, se puede hacer también con la latitud, simplemente agregando otra step_ function.
Aplicación de la discretización sobre nuevas esquinas 📍
🔎 Para hacer un caso de uso "real", se crearán 10 esquinas artificiales 🧙🏻 con la siguiente sintaxis (estamos obviando toda la complejidad y teoría detrás de la generación de datos sintéticos, es un simple ejemplo).
library(synthpop)
esquinas_artificiales <- syn(data = esquinas_plot,
m = 1,
k = 10,
seed = 123)$syn
esquinas_artificiales %>%
as_tibble() %>%
print(n_extra = 0)
# A tibble: 10 x 55
id pliegue delitos_last_ye… delitos_last_12 delitos_last_6
<fct> <int> <dbl> <dbl> <dbl>
1 esqu… 13 3 26 12
2 esqu… 13 4 44 20
3 esqu… 13 1 17 8
4 esqu… 13 1 26 16
5 esqu… 13 0 13 5
6 esqu… 13 0 8 3
7 esqu… 13 13 79 40
8 esqu… 13 4 36 17
9 esqu… 13 0 28 16
10 esqu… 13 0 20 11
# … with 50 more variables
❗ Aplicamos la receta sobre las esquinas sintéticas.
bake(Receta_xgb, new_data = esquinas_artificiales %>%
relocate(id), c(id, long))
# A tibble: 10 x 2
id long
<fct> <fct>
1 esquina_281 [-58.51,-58.49)
2 esquina_2198 [-58.41,-58.39)
3 esquina_403 [-58.48,-58.47)
4 esquina_1718 [-58.46,-58.44)
5 esquina_1659 [-58.48,-58.47)
6 esquina_617 [-58.39, Inf]
7 esquina_774 [-58.48,-58.47)
8 esquina_1764 [-58.43,-58.41)
9 esquina_2158 [-58.47,-58.46)
10 esquina_2284 [-58.51,-58.49)
✅ La columna longitud de las 10 esquinas fue discretizada en función de los rangos entrenados por la receta.
Pivot con puntos en el mapa 🗺
📌 Para fines ilustrativos, son seleccionadas las localizaciones de los estadios de Boca Juniors y River Plate.
estadios <- data.frame(lugar = c("Boca","River"),
long = c(-58.364521, -58.449715),
lat = c(-34.635706, -34.545586))
leaflet() %>% addTiles() %>%
addMarkers(data = estadios,lng = ~long, lat = ~lat)
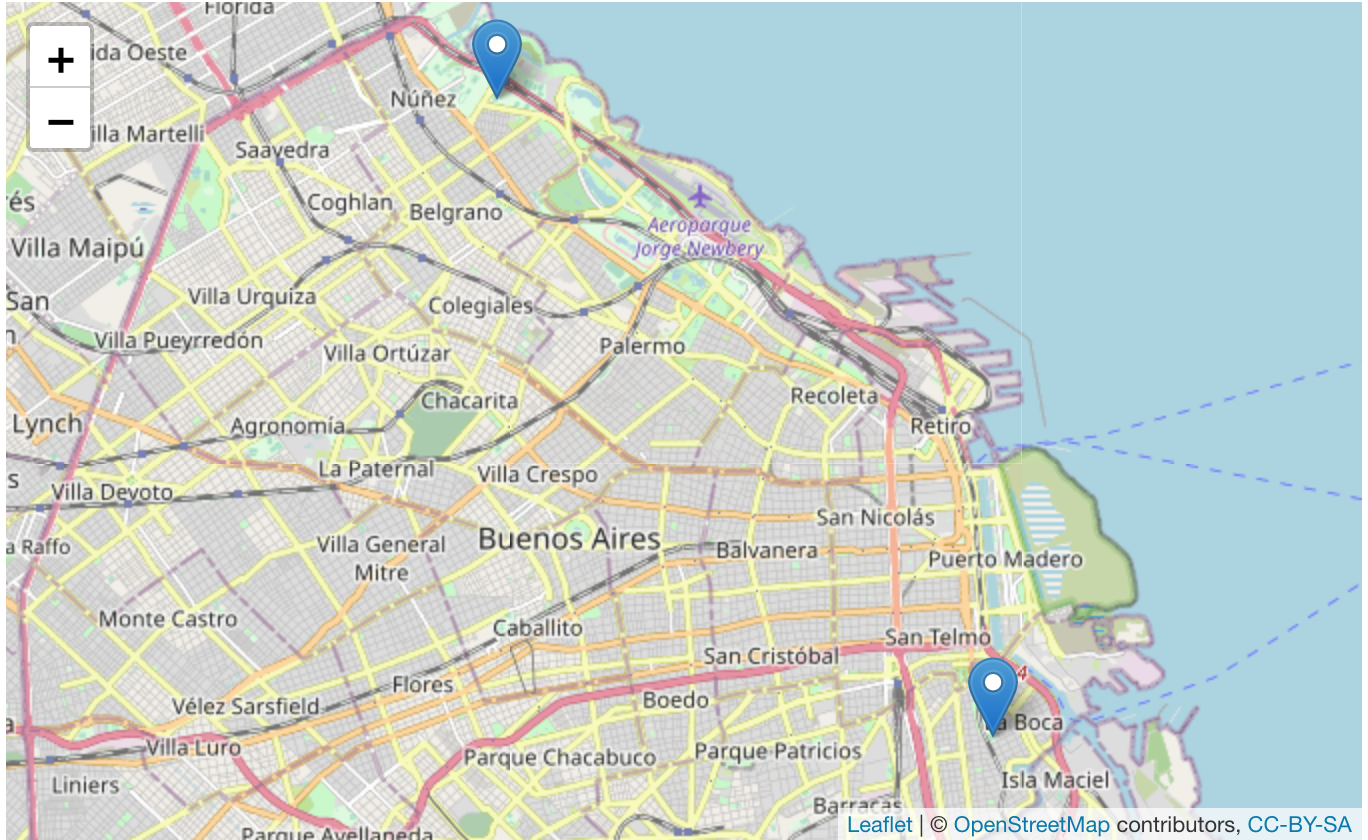
¿Cuál es el objetivo? 🤔
🔘 Se tomarán estos dos puntos en el mapa como pivote para calcular la distancia entre las esquinas y estos dos puntos.
¿Por qué?
👉🏻 Simplemente para mostrar otra herramienta de utilidad dentro de las recetas. A continuación, se aplica la función step_geodist().
Receta_pivote <- recipe(esquinas_plot) %>%
step_geodist(lat = lat, lon = long, log = FALSE, ref_lat = -34.635706,
ref_lon = -58.364521, name = "dist_boca") %>%
step_geodist(lat = lat, lon = long, log = FALSE, ref_lat = -34.545586,
ref_lon = -58.449715, name = "dist_river") %>%
prep()
🔎 La función requiere especificar cómo están nombradas lat y long en el dataset, el punto de latitud y longitud del estadio y finalmente el nombre de la variable a generar. A continuación, se hornea 🍳 la receta y se observan los resultados.
bake(Receta_pivote, new_data = esquinas_plot,
c(id, long, lat, dist_boca, dist_river)) %>% #Esta linea es solo para seleccionar columnas
print(n_extra = 0)
# A tibble: 2,023 x 5
id long lat dist_boca dist_river
<fct> <dbl> <dbl> <dbl> <dbl>
1 esquina_1 -58.5 -34.5 0.147 0.0264
2 esquina_10 -58.4 -34.6 0.0407 0.0910
3 esquina_100 -58.5 -34.6 0.138 0.0542
4 esquina_1001 -58.5 -34.6 0.157 0.0590
5 esquina_1002 -58.5 -34.6 0.150 0.0539
6 esquina_1003 -58.5 -34.6 0.158 0.0751
7 esquina_1004 -58.5 -34.6 0.156 0.0729
8 esquina_1005 -58.5 -34.6 0.158 0.0795
9 esquina_1006 -58.5 -34.6 0.157 0.0764
10 esquina_1007 -58.5 -34.6 0.152 0.0750
# … with 2,013 more rows
Uniendo todo en un workflow único 🏆
📌 Con el objetivo de mostrar el abanico de herramientas que ofrecen las recetas, se agregan de manera aleatoria algunos valores nulos en las variables de estaciones de servicio y locales gastronómicos. Posteriormente, en la receta se aplicará un método de imputación.
data_bonus <-
sknifedatar::insert_na(.dataset = data_crime_clime,
columns = c("gasolina","gastronomica"),
.p = 0.99,
seed = 123)
- Creación del modelo y partición ➗ de datos.
Modelo <- rand_forest() %>%
set_engine("ranger") %>%
set_mode("regression")
set.seed(123)
splits <- initial_split(data_bonus, prop = 0.8, strata = delitos)
splits
<Analysis/Assess/Total>
<21042/5257/26299>
- 🥘 Receta: Se utilizará como base la primera receta construida y agregaremos algunos pasos extra de preprocesamiento, incluyendo la discretización de la longitud y el pivote con los estadios de fútbol.
-
✔ Se eliminan las columnas id y pliegues. ❌
-
✔ Las variables gasolina y gastronomica presentan valores nulos, estos serán imputados a través de la mediana (no es el más indicado, se aplica por simplicidad, también están disponibles las imputación por knn y bagging).
-
✔ Se utiliza la ubicación del estadio de Boca Juniors para medir la distancia con las esquinas. 📍
-
✔ Se utiliza la ubicación del estadio de River Plate para medir la distancia con las esquinas. 📍
-
✔ Se discretiza la variable longitud, mediante un XGB en función de los delitos ocurridos en los últimos 12 meses. 📉
-
✔ Se eliminan las variables con varianza 0 (además de otras consideraciones). 🚫
-
✔ Se normalizan las variables numéricas (únicamente para fines didácticos). ⚖️
Receta <- recipe(delitos ~ ., training(splits)) %>%
step_rm(c(id,pliegue), id = "remover") %>%
step_medianimpute(all_predictors(), id = "imputación") %>%
step_geodist(lat = lat, lon = long, log = FALSE, ref_lat = -34.635706,
ref_lon = -58.364521, name = "dist_boca", id = "boca") %>%
step_geodist(lat = lat, lon = long, log = FALSE, ref_lat = -34.545586,
ref_lon = -58.449715, name = "dist_river", id="river") %>%
step_discretize_xgb(long, outcome ="delitos_last_12",
id ="xgb discet")%>%
step_nzv(all_predictors(), id = "varianza 0") %>%
step_normalize(all_numeric(), -all_outcomes(), id = "normalize")
🔎 Preparamos la receta y observamos de manera ordenada (tidy) el preprocesamiento de datos generado.
tidy(Receta %>% prep()) %>% print(n_extra = 0)
# A tibble: 7 x 6
number operation type trained skip id
<int> <chr> <chr> <lgl> <lgl> <chr>
1 1 step rm TRUE FALSE remover
2 2 step medianimpute TRUE FALSE imputación
3 3 step geodist TRUE FALSE boca
4 4 step geodist TRUE FALSE river
5 5 step discretize_xgb TRUE FALSE xgb discet
6 6 step nzv TRUE FALSE varianza 0
7 7 step normalize TRUE FALSE normalize
👉🏻 Antes de pasar la receta al flujo de modelado, ¿Puedo ver como resultaron las transformaciones en los datos?
📌 Si 🤩, simplemente con la función juice() (en realidad es un atajo para bake(Receta, new_data = train) )
Receta %>% prep() %>% juice() %>% print(n_extra = 0)
# A tibble: 21,042 x 36
delitos_last_ye… delitos_last_12 delitos_last_6 delitos_last_3
<dbl> <dbl> <dbl> <dbl>
1 0.332 1.25 0.935 0.575
2 0.102 -0.372 -0.409 -0.500
3 -0.819 -0.252 -0.222 -0.285
4 -0.589 -0.652 -0.596 -0.572
5 -0.589 -0.552 -0.409 -0.500
6 -0.589 -0.492 -0.521 -0.428
7 -0.819 -0.692 -0.596 -0.500
8 -0.128 -0.432 -0.409 -0.500
9 -0.819 -0.692 -0.783 -0.715
10 -0.358 -0.312 -0.334 -0.357
# … with 21,032 more rows, and 32 more variables
📝 Pequeño truco 👉👉 ¿Deseo ver en detalle qué columnas fueron eliminadas o creadas durante el preprocesamiento? Solo debe agregar el parámetro log_changes = TRUE a la función prep().
Receta %>% prep(log_changes = TRUE, verbose = TRUE)
# oper 1 step rm [training]
# step_rm (remover):
# removed (2): id, pliegue
#
# oper 2 step medianimpute [training]
# step_medianimpute (imputación): same number of columns
#
# oper 3 step geodist [training]
# step_geodist (boca):
# new (1): dist_boca
#
# oper 4 step geodist [training]
# step_geodist (river):
# new (1): dist_river
#
# oper 5 step discretize xgb [training]
# step_discretize_xgb (xgb discet): same number of columns
#
# oper 6 step nzv [training]
# step_nzv (varianza 0):
# removed (19): hotel_baja, hotel_alta, cine, hogares_paradores, ...
#
# oper 7 step normalize [training]
# step_normalize (normalize): same number of columns
#
# The retained training set is ~ 5.71 Mb in memory.
# Data Recipe
#
# Inputs:
#
# role #variables
# outcome 1
# predictor 54
#
# Training data contained 21042 data points and 21040 incomplete rows.
#
# Operations:
#
# Variables removed id, pliegue [trained]
# Median Imputation for delitos_last_year, ... [trained]
# Geographical distances from -34.635706 x -58.364521
# Geographical distances from -34.545586 x -58.449715
# Discretizing variables using XgBoost long [trained]
# Sparse, unbalanced variable filter removed hotel_baja, hotel_alta, ... [trained]
# Centering and scaling for delitos_last_year, ... [trained]
🔎 Se observa para cada paso las columnas eliminadas o creadas. Luego del paso 7 se muestra el siguiente mensaje “The retained training set is ~ 5.71 Mb in memory.” 🤔, esto indica el peso 💾 de la data de entrenamiento dentro de la receta.
📌 Para no guardar estos datos y hacer más liviana la receta, simplemente se especifica el argumento retain = FALSE. "Receta %>% prep(log_changes = TRUE, retain = FALSE, verbose = FALSE)".
🔹 Esto es recomendable siempre y cuando no se apliquen pasos de preprocesamiento que requieran volver a ver los datos de entrenamiento ✅, o si desea reutilizar la receta para construir recetas más avanzadas 🤖.
❗Luego, se crea un workflow, se agrega un modelo y una receta, se ajusta el workflow sobre la partición de entrenamiento. Finalmente se generan predicciones sobre la partición de prueba.
wf_fit <- workflow() %>%
add_model(Modelo) %>%
add_recipe(Receta) %>%
fit(training(splits))
wf_fit %>%
predict(testing(splits))
%>% head()
# A tibble: 6 x 1
.pred
<dbl>
1 7.04
2 0.588
3 2.82
4 1.10
5 10.5
6 21.0
🔎 Se evalúan los resultados.
resultados <- last_fit(wf_fit,splits)
collect_metrics(resultados)
# A tibble: 2 x 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 rmse standard 2.24 Preprocessor1_Model1
2 rsq standard 0.757 Preprocessor1_Model1
🎖️ Se muestran los resultados junto al dataset original.
augment(resultados) %>%
relocate(delitos,.pred, .resid) %>%
print(n_extra = 0)
# A tibble: 5,257 x 57
delitos .pred .resid id pliegue delitos_last_ye…
<dbl> <dbl> <dbl> <chr> <int> <dbl>
1 9 7.26 1.74 esqu… 1 1
2 0 0.589 -0.589 esqu… 1 0
3 2 2.73 -0.734 esqu… 1 3
4 2 1.07 0.932 esqu… 1 0
5 8 10.6 -2.64 esqu… 1 7
6 22 20.8 1.25 esqu… 1 31
7 3 3.40 -0.396 esqu… 1 2
8 1 3.38 -2.38 esqu… 1 3
9 2 2.91 -0.912 esqu… 1 1
10 0 0.957 -0.957 esqu… 1 1
# … with 5,247 more rows, and 51 more variables
Reemuestreo espacial 🌐
El último caso de uso está relacionado con partición de datos que dependen de ubicaciones geográficas 🗺. A través del siguiente ejemplo, se presenta la utilidad e importancia de este tema 🔎. Mediante la función vfold_cv(), se realiza una particion del conjunto de datos en 6 partes.
set.seed(123)
data_crime <- data_crime_clime %>% filter(pliegue == 13)
splits_crime <- vfold_cv(data_crime, strata = delitos, v = 6)
splits_crime
# 6-fold cross-validation using stratification
# A tibble: 6 x 2
splits id
<list> <chr>
1 <split [1685/338]> Fold1
2 <split [1685/338]> Fold2
3 <split [1685/338]> Fold3
4 <split [1686/337]> Fold4
5 <split [1686/337]> Fold5
6 <split [1688/335]> Fold6
¿Cómo podemos ver en el mapa las particiones de las esquinas de CABA ? 💡
Se construye la función plot_splits() (tomada de la documentación de spatialsample 📦, aunque agregando algunas mejoras) y se visualizan las 6 particiones en el mapa.
plot_splits <- function(x,y){
analysis(x) %>%
mutate(partition = "train") %>%
bind_rows(assessment(x) %>%
mutate(partition = "test")) %>%
ggplot(aes(long, lat, color = partition)) +
geom_point(alpha = 0.5) +
theme_minimal() +
labs(title = y)
}
🔹 Simplemente se aplica la función plot_splits() sobre las particiones mediante map2(), agregando una nueva columna llamada "graficos" (map, map2, pmap,.. 👉🏻👉🏻👉🏻corresponden a la familia de funciones para el desarrollo de programación funcional ordenada en R, este tema será tratado en un futuro post 🙌)
splits_crime <- splits_crime %>% mutate(graficos = map2(splits, id, plot_splits))
splits_crime
# 6-fold cross-validation using stratification
# A tibble: 6 x 3
splits id graficos
<list> <chr> <list>
1 <split [1685/338]> Fold1 <gg>
2 <split [1685/338]> Fold2 <gg>
3 <split [1685/338]> Fold3 <gg>
4 <split [1686/337]> Fold4 <gg>
5 <split [1686/337]> Fold5 <gg>
6 <split [1688/335]> Fold6 <gg>
🔹 A continuación, mediante la función ggarrange() se puede generar la visualización suministrando únicamente la columna gráficos previamente calculada.
library(ggpubr)
ggarrange(plotlist = splits_crime$graficos, common.legend = TRUE) %>%
annotate_figure(top = text_grob("Esquinas de CABA: Folds aleatorios",
color = "black", face = "bold", size = 16))
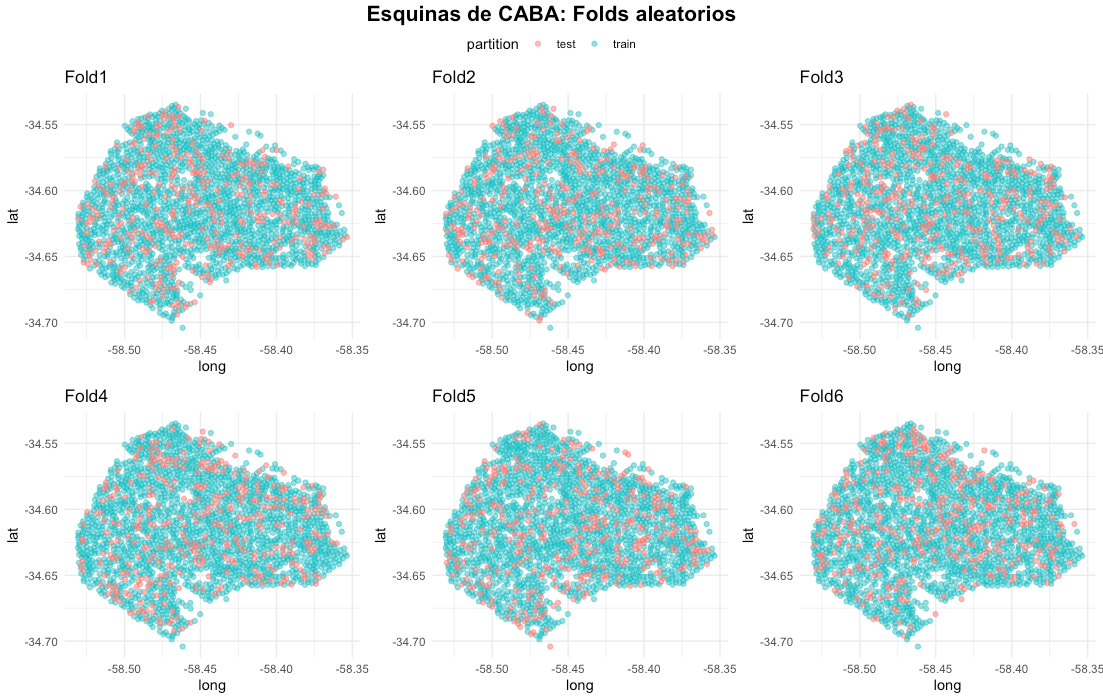
¿ Cuál es el posible problema con estas particiones? 🔎
📌 La evaluación del rendimiento de modelos predictivos de aprendizaje automático, tiene dentro de sus principios 💡 observar el rendimiento de los modelos sobre datos no utilizados durante el entrenamiento. Es decir, 👉🏻 existe un supuesto de independencia entre las observaciones de train y test.
⚠️ Sin embargo, se observa una asignación aleatoria en las particiones de entrenamiento y prueba de cada fold. Al tratarse con datos geoespaciales 🗺, está latente la existencia de autocorrelación espacial en las esquinas de CABA 🔎. Esto violaría el supuesto de independencia mencionado anteriormente 🚨.
💡 Mediante la función spatial_clustering_cv() de spatialsample 📦, puede mitigarse la autocorrelación generando particiones mediante agrupamientos de k-medias. Este es uno de los métodos más sencillos ✅, sin embargo, aún está en desarrollo la integración de técnicas más robustas al ecosistema de tidymodels.
library(spatialsample)
set.seed(123)
splits_crime <- spatial_clustering_cv(data_crime, coords = c("lat", "long"), v = 6)
splits_crime
# 6-fold spatial cross-validation
# A tibble: 6 x 2
splits id
<list> <chr>
1 <split [1713/310]> Fold1
2 <split [1712/311]> Fold2
3 <split [1744/279]> Fold3
4 <split [1619/404]> Fold4
5 <split [1653/370]> Fold5
6 <split [1674/349]> Fold6
🔹 Siguiendo el caso aleatorio, se aplica la función plot_splits() para observar las particiones en el mapa.
splits_crime <- splits_crime %>% mutate(graficos = map2(splits, id, plot_splits))
ggarrange(plotlist = splits_crime$graficos, common.legend = TRUE) %>%
annotate_figure(
top =text_grob("Esquinas de CABA: Folds K-means",
color = "black", face = "bold", size = 16)
)
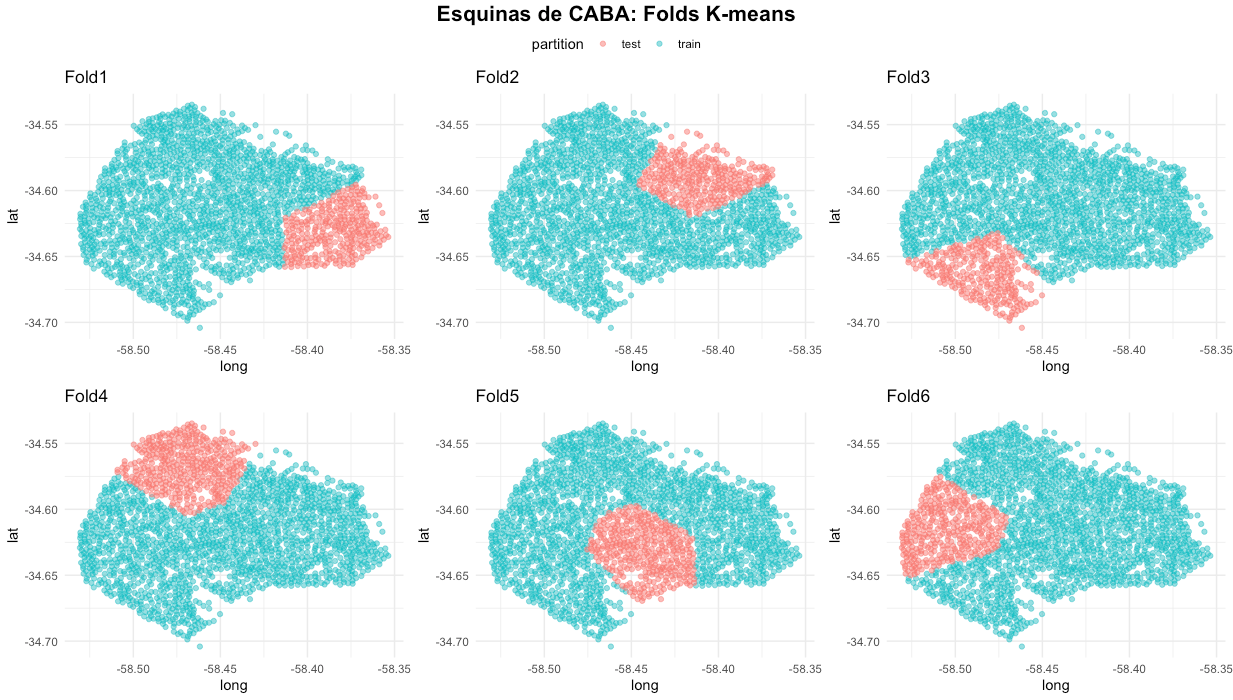
🔹 Se observa un contraste importante entre las 2 particiones. Visualmente, es bastante intuitivo entender las diferencias y aplicaciones de ambos enfoques.
📍 A modo de ejemplo, se evaluará el rendimiento de un modelo de random forest 🤖mediante un workflow 🔁 sobre las 6 particiones. Para esto se creará la función predict_folds() tomada del ejemplo de la documentación de spatialsample 📦, pero con algunas adaptaciones 🛠 para poder incorporar un workflow, la función hace lo siguiente:
-
✔ Crea un modelo 🤖.
-
✔ Crea una receta 🍳.
-
✔ Guarda todo en un workflow y se ajusta sobre la parte de train de un fold 🚀.
-
✔ Realiza predicciones sobre la parte de test 🔮.
predict_folds <- function(x) {
modelo <- rand_forest() %>%
set_engine("ranger") %>%
set_mode("regression")
receta <- recipe(delitos ~ ., data = analysis(x)) %>%
step_rm(c(id,pliegue), id = "remover")
workflow_crime <- workflow() %>%
add_model(modelo) %>%
add_recipe(receta) %>%
fit(analysis(x))
test <- assessment(x)
tibble::tibble(Longitude = test$long,
Latitude = test$lat,
observed = test$delitos,
predict(workflow_crime, test))
}
🔹 Se aplica la función tal sobre cada partición mediante map().
folds_crime <- splits_crime %>% mutate(predictions = map(splits, predict_folds))
🔹 Se calcula la métrica mae para cada partición.
folds_crime_mae <- folds_crime %>%
unnest(predictions) %>%
group_by(id) %>%
mae(observed, .pred)
folds_crime_mae
# A tibble: 6 x 4
id .metric .estimator .estimate
<chr> <chr> <chr> <dbl>
1 Fold1 mae standard 2.06
2 Fold2 mae standard 2.60
3 Fold3 mae standard 1.25
4 Fold4 mae standard 1.32
5 Fold5 mae standard 1.48
6 Fold6 mae standard 1.14
🔹 Se visualizan las particiones y su rendimiento de manera conjunta sobre el mapa.
folds_crime %>%
unnest(predictions) %>%
left_join(folds_crime_mae) %>%
ggplot(aes(Longitude, Latitude, color = .estimate)) +
geom_point(alpha = 0.5) +
labs(color = "MAE") +
theme_minimal()
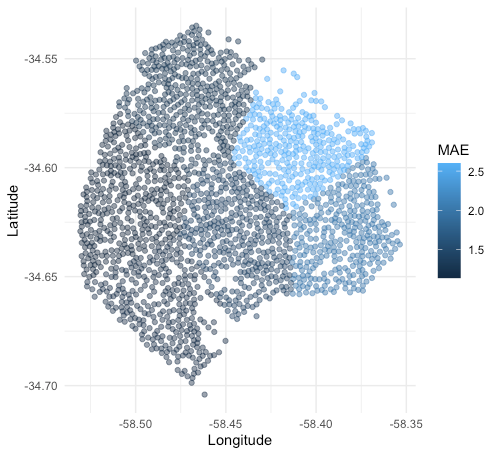
⚠️ No se está realizando un ajuste de hiperparámetros, tampoco un proceso de selección de variables. 👉🏻 Simplemente es un ejemplo didáctico para explicar la utilidad y precauciones que deben tomarse al trabajar con datos geoespaciales 🌐.
Comentarios finales ✍🏻
🔘 El ecosistema tidymodels, representa un cambio disruptivo 🚀 para el análisis de datos en R. La mayoría de los nuevos desarrollos 💡 de modelado predictivo se están desarrollando sobre este ecosistema (series de tiempo 📈, supervivencia 📆, estadística bayesiana 🧪, cluster 💠, SDK para el despliegue en cloud ☁,...).
👉🏻 En esta serie de posts, se intenta explicar (con suerte 🤣) como utilizar tidymodels, mostrando la lógica general de su funcionamiento y posteriormente presentando casos de uso avanzados sobre datos geoespaciales 🌐.
Muchas gracias por leernos 👏🏻👏🏻👏🏻.
Siéntase libre de comentar y compartir 👌🏻.
Por Rafael Zambrano - Contacto: LinkedIn / Twitter / Blog-Post


